We will begin from the N-slit diffraction pattern derived on the diffraction page.
![\psi ={{\psi }_0}\left[\frac{\sin \left(\frac{{\pi a}}{\lambda }\sin\theta \right)}{\frac{{\pi a}}{\lambda }\sin\theta}\right]\left[\frac{\sin \left(\frac{N}{2}{kd}\sin\theta\right)}{\sin \left(\frac{{kd}}{2}\sin\theta \right)}\right]](http://upload.wikimedia.org/math/5/c/e/5ced075993b8410cdf357c301b644b88.png)
Now, adding a φ term to the 
fringe effect in the second term yields:
![\psi ={{\psi }_0}\left[\frac{\sin \left(\frac{{\pi a}}{\lambda }\sin \theta\right)}{\frac{{\pi a}}{\lambda }\sin\theta}\right]\left[\frac{\sin \left(\frac{N}{2}\big(\frac{{2\pi d}}{\lambda }\sin\theta + \phi \big)\right)}{\sin \left(\frac{{\pi d}}{\lambda }\sin\theta +\phi \right)}\right]](http://upload.wikimedia.org/math/2/d/3/2d37c7be4f9b566214bc13a290439570.png)
Taking the square of the wave function gives us the intensity of the wave.
![I = I_0{{\left[\frac{\sin \left(\frac{\pi a}{\lambda }\sin\theta\right)}{\frac{{\pi a}}{\lambda } \sin [\theta ]}\right]}^2}{{\left[\frac{\sin \left(\frac{N}{2}(\frac{2\pi d}{\lambda} \sin\theta+\phi )\right)}{\sin \left(\frac{{\pi d}}{\lambda } \sin\theta+\phi \right)}\right]}^2}](http://upload.wikimedia.org/math/1/3/3/1332e02f034201f7bc0d3de036e3c27c.png)
![I =I_0{{\left[\frac{\sin \left(\frac{{\pi a}}{\lambda } \sin\theta\right)}{\frac{{\pi a}}{\lambda } \sin\theta}\right]}^2}{{\left[\frac{\sin \left(\frac{\pi }{\lambda } N d \sin\theta+\frac{N}{2} \phi \right)}{\sin \left(\frac{{\pi d}}{\lambda } \sin\theta+\phi \right)}\right]}^2}](http://upload.wikimedia.org/math/3/5/3/353b4dcb6b13c5cc3095a185910ff5d6.png)
Now space the emitters a distance 
apart. This distance is chosen for simplicity of calculation but can be adjusted as any scalar fraction of the wavelength.
![I =I_0{{\left[\frac{\sin \left(\frac{\pi }{\lambda } a \theta \right)}{\frac{\pi }{\lambda } a \theta }\right]}^2}{{\left[\frac{\sin \left(\frac{\pi }{4} N \sin\theta+\frac{N}{2} \phi \right)}{\sin \left(\frac{\pi }{4} \sin\theta+ \phi \right)}\right]}^2}](http://upload.wikimedia.org/math/1/d/a/1da053851c4c364b2dc3a87770813193.png)
Sin achieves its maximum at 
so we set the numerator of the second term = 1.
Thus as N gets large, the term will be dominated by the 
term. As sin can oscillate between −1 and 1, we can see that setting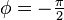 
will send the maximum energy on an angle given by
Additionally, we can see that if we wish to adjust the angle at which the maximum energy is emitted, we need only to adjust the phase shift φ between successive antennas. Indeed the phase shift corresponds to the negative angle of maximum signal.
A similar calculation will show that the denominator is minimized by the same factor.
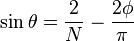
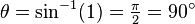
Tiada ulasan:
Catat Ulasan